Skip to contents

Functions for gastric emptying analysis

Source: R/fitfuncs.r
gastemptfunc.Rd

The linexp and the power exponential (powexp) functions can be used to fit gastric emptying curves.

Usage

linexp(t, v0 = 1, tempt = NULL, kappa = NULL, pars = NULL)

linexp_slope(t, v0 = 1, tempt = NULL, kappa = NULL, pars = NULL)

linexp_auc(v0 = 1, tempt = NULL, kappa = NULL, pars = NULL)

powexp(t, v0 = 1, tempt = NULL, beta = NULL, pars = NULL)

powexp_slope(t, v0 = 1, tempt = NULL, beta = NULL, pars = NULL)

linexp_log(t, v0 = 1, logtempt = NULL, logkappa = NULL, pars = NULL)

powexp_log(t, v0 = 1, logtempt = NULL, logbeta = NULL, pars = NULL)

Arguments

t

Time after meal or start of scan, in minutes; can be a vector.

v0

Initial volume at t=0.

tempt

Emptying time constant in minutes (scalar).

kappa

Overshoot term for linexp function (scalar).

pars

Default NULL. If not NULL, the other parameters with exception of t are not used and are retrieved as named parameters from the numeric vector pars instead.

beta

Power term for power exponential function (scalar).

logtempt

Logarithm of emptying time constant in minutes (scalar).

logkappa

Logarithm of overshoot term for linexp function (scalar).

logbeta

Logarithm of power term for power exponential function (scalar).

Value

Vector of length(t) for computed volume.

Details

The linexp function can have an initial overshoot to model secretion.

vol(t) = v0 * (1 + kappa * t / tempt) * exp(-t / tempt)

The powexp function introduced by Elashof et al. is montonously decreasing but has more freedom to model details in the function tail.

vol(t) = v0 * exp(-(t / tempt) ^ beta)

The _slope functions return the first derivatives of linexp and powexp. Use the _log functions to enforce positive parameters tempt and beta. Rarely required for gastric emptying curves.

Examples

t = seq(0,100, by=5)
kappa = 1.3
tempt = 60
v0 = 400
beta = 3
pars = c(v0 = v0, tempt = tempt, kappa = kappa)
oldpar = par(mfrow = c(1,3))
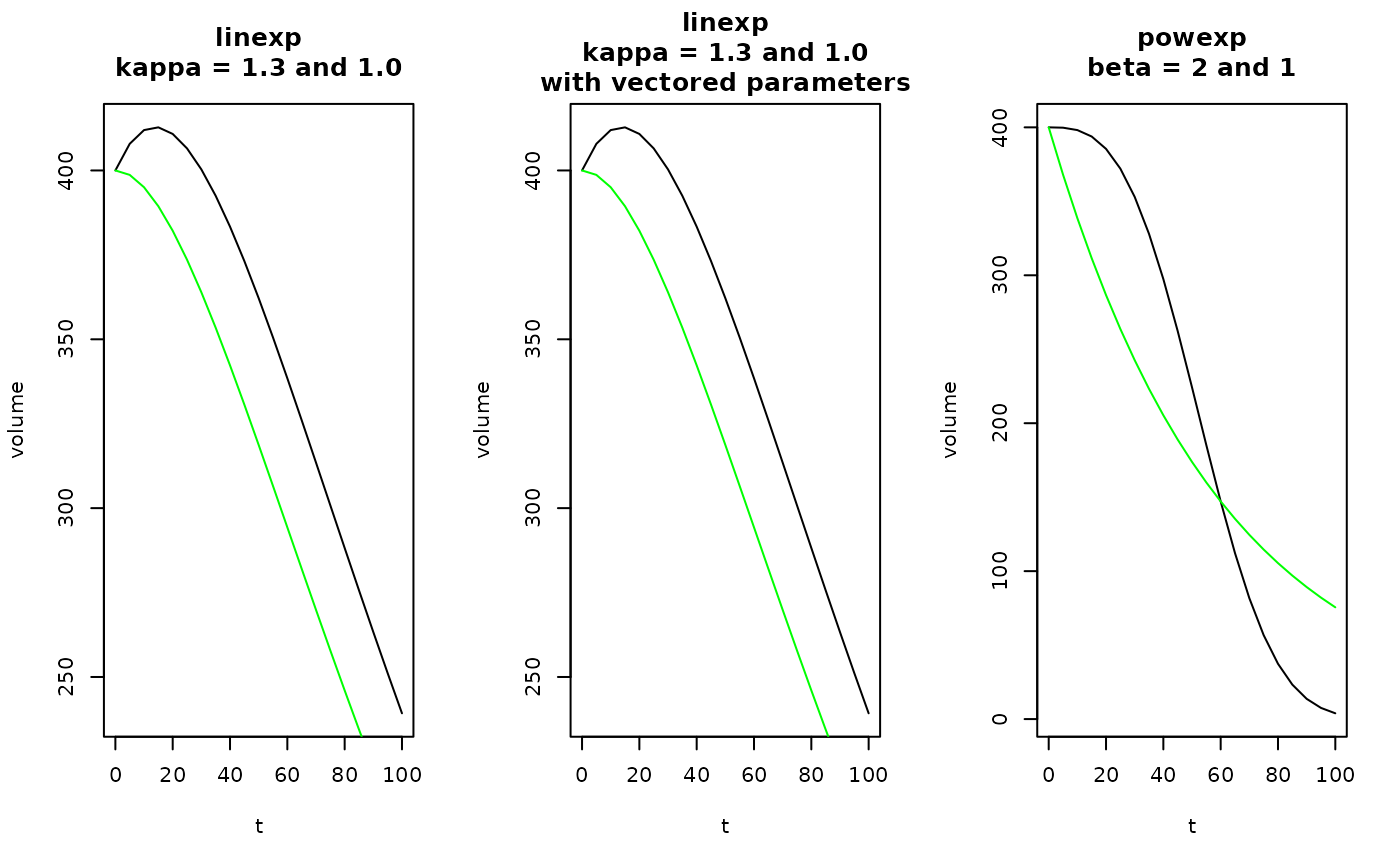
plot(t, linexp(t, v0, tempt, kappa), type = "l", ylab = "volume",
   main = "linexp\nkappa = 1.3 and 1.0")
lines(t, linexp(t, v0, tempt, 1), type = "l", col = "green")
# This should give the same plot as above
plot(t, linexp(t, pars = pars), type = "l", ylab = "volume",
   main = "linexp\nkappa = 1.3 and 1.0\nwith vectored parameters")
lines(t, linexp(t, v0, tempt, 1), type = "l", col = "green")
plot(t, powexp(t, v0, tempt, beta), type = "l", ylab = "volume",
  main = "powexp\nbeta = 2 and 1")
lines(t, powexp(t, v0, tempt, 1), type = "l", col = "green")

par(oldpar)